2020_java蓝桥_暑假训练_递归

发表于 | 分类于 ， | 热度: ℃
字数统计: 3.8k | 阅读时长 ≈ 16

🌸递归训练

🌸The_39_Steps

🍁1、小明刚刚看完电影《第39级台阶》。离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!

站在台阶前，他突然又想着一个问题：

如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？

请你利用计算机的优势，帮助小明寻找答案。

分析

根据题目要求，一次只能，迈出一步或者两步，第一脚是左脚，最后一脚是右脚，这意味着自己走的步数只能是偶数，递归思想思考题目，39级台阶的走法应该是从37级台阶或者38级台阶走上来的，即39级走法等于37级走法加上38级走法的总和，以此一直倒推，……..走到第三级台阶是从第第一级和第二级上来的，当台阶只剩下2级，无论你之前走了奇数步还是偶数步，都能有一种走法实现总和步数是偶数步，所以这里可以作为递归出口之一，直接return 1;，当台阶只剩下一步，由于总步数只能是偶数步，所以之前的步数只能是奇数步才能满足条件，return 1，偶数步则走法不符合题意。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class The_39_Steps {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n = input.nextInt();
		System.out.println(steps(n, 0));
		input.close();
	}
	public static int steps(int n, int count) {
		if(n == 1) {
			if(count % 2 == 0) {
				return 0;
			}
			return 1;
		}
		if(n == 2) {
			return 1;
		}
		
		return steps(n - 1, count + 1) + steps(n - 2, count + 1);
	}
}

🌸Motorcade_checkpoint

🍁2、X星球特别讲究秩序，所有道路都是单行线。

一个甲壳虫车队，共16辆车，按照编号先后发车，夹在其它车流中，缓缓前行。

路边有个死胡同，只能容一辆车通过，是临时的检查站，如图所示。

aoLxxA.png

X星球太死板，要求每辆路过的车必须进入检查站，也可能不检查就放行，也可能仔细检查。

如果车辆进入检查站和离开的次序可以任意交错。那么，该车队再次上路后，可能的次序有多少种？

为了方便起见，假设检查站可容纳任意数量的汽车。

显然，如果车队只有1辆车，可能次序1种；2辆车可能次序2种；3辆车可能次序5种。

分析

这道题看似十分绕。但是把检查站看成一个这题就变成了一个列表求出栈的次序数问题，每一种操作有两种情况，进站和出站，一辆车在检查站没有车的情况下只能选择进站，一辆车在检查站有车的情况下有

  • 进站，检查站车辆数目加一
  • 不进站，检查站检查车辆，车辆出站，检查站车辆数目减一

出站次序数即上面；两种情况之和

利用n 代表正在等候进站的车辆数目，m代表检查站车辆数目，当n 为0时递归可结束详情见代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Motorcade_checkpoint {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n = input.nextInt();
		System.out.println(check(n, 0));
		input.close();
	}
	private static int check(int n, int m) {
		if(n == 0) {//如果左边没有车
			return 1;
		}
		if(m == 0) {//如果检查站没有车
			return check(n - 1, 1);
		}
		if(m > 0) {//如果检查站有车取决于车辆是入还是出
			return check(n - 1, m + 1) + check(n, m - 1);
		}
		return 0;
	}	
}

🍁解法二：回溯（DFS）

求解排列问题一把想到的就是回溯剪枝。题中，只有站中有车，车辆才会被允许出站，假设1代表进站，0代表出站，r代表进站的个数，l代表出站的个数，即只有当进站的个数大于等于出站的个数才可以进站或者出站，否则只能进站。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Motorcade_checkpoint {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n = input.nextInt();
		dfs(0, 0, 0);
		System.out.println(num);
		input.close();
	}
	private static int num = 0;
	private static void dfs(int n, int r, int l) {
		if(n == 32) {
			num++;
			return;
		}
		if(r > l) {
			if(r < 16) {
				dfs(n + 1, r + 1, l);
			}
			if(l < 16) {
				dfs(n + 1, r, l + 1);
			}
		}else {
			if(r == l || r < 16) {
				dfs(n + 1, r + 1, l);
			}
		}
		return;
	}	
}

🍁解法三：数学推理

我们把n个元素的出栈个数的记为f(n), 那么对于1,2,3, 我们很容易得出

1
2
3
4
5
f(1)= 1   //即 1
	
f(2)= 2   //即 12、21
	
f(3)= 5   //即 123、132、213、321、231

然后我们来考虑f(4), 我们给4个元素编号为a,b,c,d, 那么考虑：元素a只可能出现在1号位置，2号位置，3号位置和4号位置(很容易理解，一共就4个位置，比如abcd,元素a就在1号位置)。

🍁分析：

​ 1) 如果元素a在1号位置，那么只可能a进栈，马上出栈，此时还剩元素b、c、d等待操作，就是子问题f(3)；
​
​ 2) 如果元素a在2号位置，那么一定有一个元素比a先出栈，即有f(1)种可能顺序（只能是b），还剩c、d，即f(2)， 根据乘法原理，一共的顺序个数为f(1)* f(2)；
​
​ 3) 如果元素a在3号位置，那么一定有两个元素比1先出栈，即有f(2)种可能顺序（只能是b、c），还剩d，即f(1)，
​
​ 根据乘法原理，一共的顺序个数为f(2) * f(1)；
​
​ 4) 如果元素a在4号位置，那么一定是a先进栈，最后出栈，那么元素b、c、d的出栈顺序即是此小问题的解，即 f(3)；
​
​ 结合所有情况，即f(4) = f(3) +f(2) * f(1) + f(1) * f(2) + f(3);
​
​ 为了规整化，我们定义f(0) = 1；于是f(4)可以重新写为：
​
​ f(4) = f(0) * f(3) + f(1) * f(2) + f(2) * f(1)+ f(3) * f(0)
​
​ 然后我们推广到n，推广思路和n=4时完全一样，于是我们可以得到：
​
​ f(n) = f(0) * f(n-1) + f(1) * f(n-2) + … +f(n-1) * f(0)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Motorcade_checkpoint {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n = input.nextInt();
		System.out.println(catalan(n));
		input.close();
	}
	private static int catalan(int n) {
		int[] cal = new int[n + 1];
		cal[0] = 1;
		cal[1] = 1;
		cal[2] = 2;
		cal[3] = 5;
		for(int i = 4; i <= n; i++) {
			for(int j = 0; j <= i - 1; j++) {
				cal[i] += cal[j] * cal[i - 1 - j];
			}
		}
		return cal[n];
	}	
}

🍁解法四：卡塔兰序列

根据解法三，最后的序列其实是卡塔兰序列，

令h(0)=1,h(1)=1，卡塔兰数满足递归式:
h(n)= h(0)*h(n-1) + h(1)*h(n-2) + .. + h(n-1)h(0) (其中n>=2),这是n阶递推关系;
还可以化简为1阶递推关系:如h(n)=(4n-2)/(n+1)*h(n-1)(n>1) h(0)=1
该递推关系的解为:
$$
h(n)=\frac{C(2n,n)}{n+1}=\frac{P(2n,n)}{(n+1)!}=\frac{(2n!)}{(n!*(n+1)!)}(n=1,2,3,…)
$$

$$
C_n = \frac{(2n)!}{(n+1)!n!}
$$

$$
C_0=1, C_{n+1} = \frac{2(2n+1)}{n+2}C_n
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Motorcade_checkpoint {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n = input.nextInt();
		System.out.println(catalan2(n));
		input.close();
	}
	private static int catalan2(int n) {
		int[] cal = new int[n + 1];
		cal[0] = 1;
		cal[1] = 1;
		for(int i = 2; i <= n; i++) {
			cal[i] = cal[i - 1]*(4*i - 2) / (i + 1);
		}
		return cal[n];
	}	
}

🌸Equation

3、匪警请拨110,即使手机欠费也可拨通！

为了保障社会秩序，保护人民群众生命财产安全，警察叔叔需要与罪犯斗智斗勇，因而需要经常性地进行体力训练和智力训练！

某批警察叔叔正在进行智力训练：

1 2 3 4 5 6 7 8 9 = 110

请看上边的算式，为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法；123+4+5+67-89 是另一个可能的答案。

请你利用计算机的优势，帮助警察叔叔快速找到所有答案。

每个答案占一行。形如：

12+34+56+7-8+9

123+4+5+67-89

……

🍁分析

用暴力思路去分析很好理解，就是从1开始逐渐往后面添加符号’+’或’-‘，直到添加到9时将整个式子进行检查，查看是否是我们需要的式子，如果是，则输出。否则跳过进行下一层的递归递归其实就是利用递归的方式去实现暴力解法详情看代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Equation {
	public static void main(String[] args) {
		String str = "123456789";
		func(str, 1);
	}
	private static void func(String v, int n) {
		//递归结束条件修改到最后一位时输出
		if(n == 9) {
			check(v);
		}else { // 递归向后修改，数字中间加上符号
			func(v.replace(n + "", n + "+"), n + 1);
			func(v.replace(n + "", n + "-"), n + 1);
			func(v, n + 1);
		}
	}
    /**
	 * 验证字符串函数
	 * @param str
	 */
	private static void check(String str) {
		String[] s = str.split("[\\+]");
		int sum = 0;
		for(String t : s) {
			String[] sub = t.split("[\\-]");
			int num = Integer.parseInt(sub[0]);
			//计算负数
			for(int i = 1; i < sub.length; i++) {
				num -= Integer.parseInt(sub[i]);
			}
			sum += num; // 正数或负数结果加到总和上去
		}
		if(sum == 110) {
			System.out.println(str);
		}
	}
}

🍁解法二：直接遍历（暴力解法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class Equation {
	public static void main(String[] args) {
		String str = "123456789";
		fun(str);
	}
    // 遍历所有情况
	public static void fun(String s) {
		char[] c = s.toCharArray();
		StringBuffer sb = new StringBuffer();	// 记录 组成的式子
		int len = s.length()-1;	// 字符串长度 - 1	
		int[] sign = new int[len];	// sign用来标记符号, 最多有（s的长度-1）个符号
		// 从后身前添加符号
		while(sign[0]<3){	// 最前面的判定符号的值若 >=3 则结束循环	
			sb.append(c[0]);	// 添加首元素
			for(int i=0;i<len;i++){
				if(sign[i]==1){		// 值为1添加"+"号
					sb.append("+");
				}else if(sign[i]==2){// 值为2添加"-"号
					sb.append("-");
				}
				sb.append(c[i+1]);	// 不管添加不添加+-号，都添加后一个元素
			}
			
			check2(sb.toString());	// 验证并输出
			
			sb.setLength(0);	// 清空sb
			sign[len-1]++;	// 每循环一次，最后一个符号值加1
			for(int i=len-1;i>0;i--){	//当值等于3时，实现逢3进位
				if(sign[i]==3){
					sign[i] = 0;	// sign[i] 归零
					sign[i-1]++;	// sign[i-1]进位
				}
			}
		}
	}
	// 验证并输出
	public static void check2(String str){
		String[] s = str.split("[\\+]|[-]");	// 得到全部数字
		String sign = str.replaceAll("\\d*", "");	// 得到全部符号（+-）
		int sum = Integer.parseInt(s[0]);	// 把第一个数字给sum
		for(int i=0;i<s.length-1;i++){
			switch(sign.charAt(i)){
				case '+': 
					sum += Integer.parseInt(s[i+1]);
					break;
				case '-': 
					sum -= Integer.parseInt(s[i+1]);
					break;
			}
		}
		if(sum==110){	// 符合条件输出
			System.out.println(str);
		}
	}
}

🌸Bus_Fare

4、公园票价为5角。假设每位游客只持有两种币值的货币：5角、1元。

再假设持有5角的有m人，持有1元的有n人。

由于特殊情况，开始的时候，售票员没有零钱可找。

我们想知道这m+n名游客以什么样的顺序购票则可以顺利完成购票过程。

显然，m < n的时候，无论如何都不能完成；

m>=n的时候，有些情况也不行。比如，第一个购票的乘客就持有1元。

请计算出这m+n名游客所有可能顺利完成购票的不同情况的组合数目。

注意：只关心5角和1元交替出现的次序的不同排列，持有同样币值的两名游客交换位置并不算做一种新的情况来计数。

🍁分析

这道题就这么看，确实难找，m, n 难找，那么就去找fun(m - 1, n)和fun(m, n - 1)逐个去分析，分别去掉一个拿5毛的和一个拿一元的，然后再将这两种情况相加，最后如果m<n，说明无解，返回0如果n==0，那一定只有一种情况，因为所有人都拿5毛了，如果拿5毛的比拿1块的还要多或者相等，那可以继续递归下去，这样将所有的情况相加，就可以得到所有的可能了，其实这是一个模拟人来等车的过程，假如一开始一个人都没有，那么，每过一个时刻，我们让一个人来排队，这个人可能拿5毛，可能拿一块，最后总共来了m+n个人，而所有的情况相加就可以得到答案，可以看出，递归实际上是从结果到开始状态，也就是倒着递推，来找到所有的情况的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Bus_Fare {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int m = input.nextInt();
		int n = input.nextInt();
		System.out.println(fun(m, n));
		input.close();
	}
	private static int fun(int m, int n) {
		if(m < n) {
			return 0;
		}
		if(n == 0) {
			return 1;
		}
		return fun(m - 1, n) + fun(m, n - 1);
	}
	
}

🌸Jump_Lattice

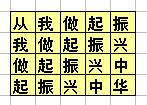
5、小明参加了学校的趣味运动会，其中的一个项目是：跳格子。

地上画着一些格子，每个格子里写一个字，如下所示：（也可参见下图）

aTB8NF.png

比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。

要求跳过的路线刚好构成“从我做起振兴中华”这句话。

请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

🍁分析

模拟遍历二维矩阵，从左上角落（0,0）出发，只能向右或者向下（向左向上不满足题意）直到右下角（3, 4）结束。由于此题并未用到矩阵中的任何数据而且矩阵具有特殊性，从左上角到右下角无论向右还是向下的任何一条路径都满足题意，只是求路径的个数。所以此题并不需要借助矩阵，只需要写个遍历方式即可，当矩阵x点小于目标x,使点向右移动，当点y小于目标y值，将点向下移动，当（x, y）等于目标的（x, y）则路径加1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Jump_Lattice {
	private static int path = 0;
	public static void main(String[] args) {
		dfs(0, 0, 3, 4);
		System.out.println(path);
	}
	private static void dfs(int startX, int startY, int endX, int endY) {
		if(startX == endX && startY == endY) {
			path++;
		}
		if(startX < endX) {
			dfs(startX + 1, startY, endX, endY);
		}
		if(startY < endY) {
			dfs(startX, startY + 1, endX, endY);
		}
	}	
}

🍁解法二：动态规划

同递归思路倒推，点（3, 4）的路径数来自点（2, 4）和（3, 3）；（其中边缘路径只能来自一个地方，所以需要初始化边缘路径数为1即dp[0] [j] = 1和dp[i] [0] = 1）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Jump_Lattice {
	public static void main(String[] args) {
		//dp
		int[][] dp = new int[4][5];
		for(int i = 0; i < 4; i++) {
			dp[i][0] = 1;
		}
		for(int j = 0; j < 5; j++) {
			dp[0][j] = 1;
		}
		for(int i = 1; i < 4; i++) {
			for(int j = 1; j < 5; j++) {
				dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
			}
		}
		System.out.println(dp[3][4]);
		
	}
}

最后，不经历风雨,怎能在计算机的大山之顶看见彩虹呢！ 无论怎样，相信明天一定会更好！！！！！

-------------本文结束感谢您的阅读-------------
云澈 wechat
扫一扫，用手机访问哦
坚持原创技术分享，您的支持将鼓励我继续创作！
0%