回溯_leetcode.60.第k个排列

发表于 | 分类于 ， | 热度: ℃
字数统计: 1.6k | 阅读时长 ≈ 6

🌸题目

🍁给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

1
2
3
4
5
6
"123"
"132"
"213"
"231"
"312"
"321"

给定 n 和 k，返回第 k 个排列。

说明：

  • 给定 n 的范围是 [1, 9]。
  • 给定 k 的范围是[1, n!]。

示例 1:

1
2
输入: n = 3, k = 3
输出: "213"

示例 2:

1
2
输入: n = 4, k = 9
输出: "2314"

🌸分析

以下给出了两种方法，思路其实是一样的：通过 计算剩余数字个数的阶乘数，一位一位选出第 k 个排列的数位。

🌸解法一：DFS+剪枝

容易想到，使用同「力扣」第 46 题： 全排列 的回溯搜索算法，依次得到全排列，输出第 k 个全排列即可。事实上，我们不必求出所有的全排列。

基于以下几点考虑：

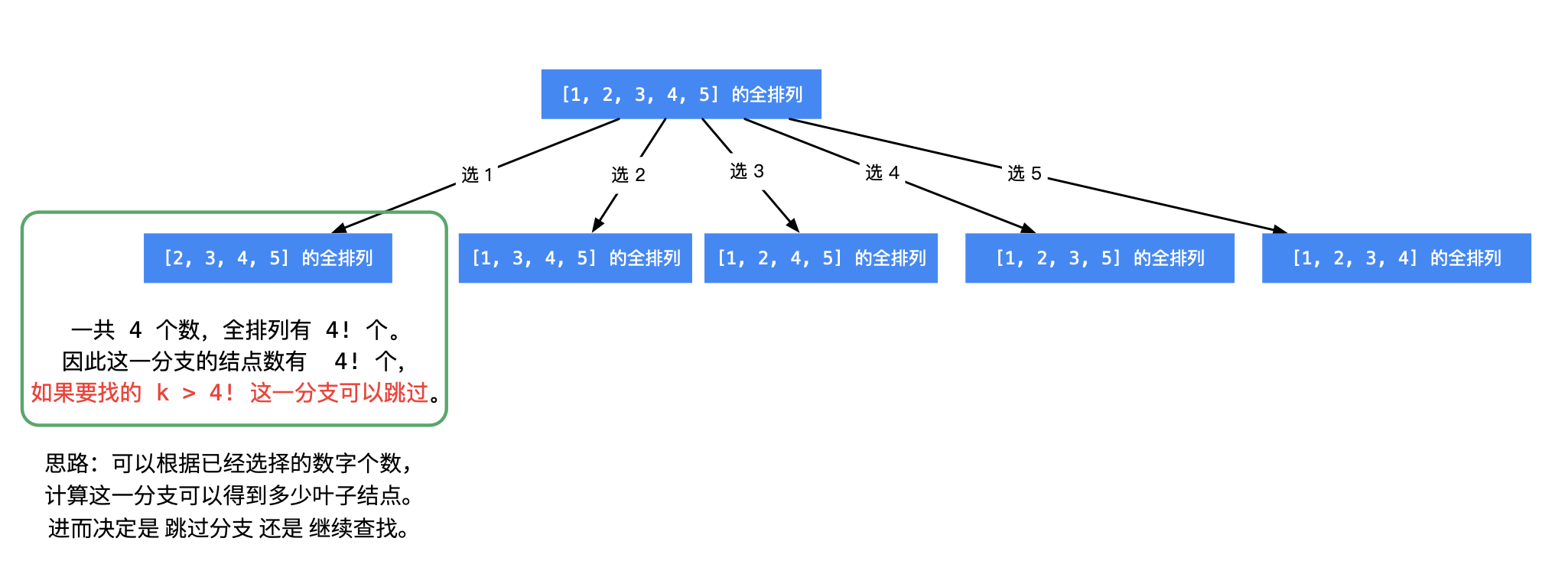
  • 所求排列 一定在叶子结点处得到，进入每一个分支，可以根据已经选定的数的个数，进而计算还未选定的数的个数，然后计算阶乘，就知道这一个分支的 叶子结点 的个数：
    • 如果 k 大于这一个分支将要产生的叶子结点数，直接跳过这个分支，这个操作叫「剪枝」；
    • 如果 k 小于等于这一个分支将要产生的叶子结点数，那说明所求的全排列一定在这一个分支将要产生的叶子结点里，需要递归求解。

编码注意事项：

  • 计算阶乘的时候，可以使用循环计算。注意：0!=1，它表示了没有数可选的时候，即表示到达叶子结点了，排列数只剩下 1个；
  • 题目中说「给定 n 的范围是 [1, 9]」，可以把从 0到 9 的阶乘计算好，放在一个数组里，可以根据索引直接获得阶乘值；
  • 编码的时候，+1 还是 -1 ，大于还是大于等于，这些不能靠猜。常见的做法是：代入一个具体的数值，认真调试。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
import java.util.Arrays;

public class Solution {

    /**
     * 记录数字是否使用过
     */
    private boolean[] used;

    /**
     * 阶乘数组
     */
    private int[] factorial;

    private int n;
    private int k;

    public String getPermutation(int n, int k) {
        this.n = n;
        this.k = k;
        calculateFactorial(n);

        // 查找全排列需要的布尔数组
        used = new boolean[n + 1];
        Arrays.fill(used, false);

        StringBuilder path = new StringBuilder();
        dfs(0, path);
        return path.toString();
    }


    /**
     * @param index 在这一步之前已经选择了几个数字，其值恰好等于这一步需要确定的下标位置
     * @param path
     */
    private void dfs(int index, StringBuilder path) {
        if (index == n) {
            return;
        }

        // 计算还未确定的数字的全排列的个数，第 1 次进入的时候是 n - 1
        int cnt = factorial[n - 1 - index];
        for (int i = 1; i <= n; i++) {
            if (used[i]) {
                continue;
            }
            if (cnt < k) {
                k -= cnt;
                continue;
            }
            path.append(i);
            used[i] = true;
            dfs(index + 1, path);
            // 注意 1：没有回溯（状态重置）的必要

            // 注意 2：这里要加 return，后面的数没有必要遍历去尝试了
            return;
        }
    }

    /**
     * 计算阶乘数组
     *
     * @param n
     */
    private void calculateFactorial(int n) {
        factorial = new int[n + 1];
        factorial[0] = 1;
        for (int i = 1; i <= n; i++) {
            factorial[i] = factorial[i - 1] * i;
        }
    }
}

python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def getPermutation(self, n: int, k: int) -> str:
        def dfs(n, k, index, path):
            if index == n:
                return
            cnt = factorial[n - 1 - index]
            for i in range(1, n + 1):
                if used[i]:
                    continue
                if cnt < k:
                    k -= cnt
                    continue
                path.append(i)
                used[i] = True
                dfs(n, k, index + 1, path)
                # 注意：这里要加 return，后面的数没有必要遍历去尝试了
                return

        if n == 0:
            return ""

        used = [False for _ in range(n + 1)]
        path = []
        factorial = [1 for _ in range(n + 1)]
        for i in range(2, n + 1):
            factorial[i] = factorial[i - 1] * i

        dfs(n, k, 0, path)
        return ''.join([str(num) for num in path])

  • 时间复杂度：O({N^2})，

  • 空间复杂度：O(N)，nums、used、path 都与 N 等长，factorial 数组就 10个数，是常数级别的。

k -= cnt; 这一步，每一次剪枝太慢，事实上，可以用除法加快这一步骤。但是需要维护一个有序数组（或者链表），时间复杂度不变。

🌸解法二：有序数组（链表）模拟

以 n = 4，k = 6，为例，现在确定第 1 个数字填啥。如果第 k个数恰好是后面的数字个数的阶乘，那么第 1 个数字就只能填最小的 1。

如果 n = 4，k = 16，现在确定第 1 个数字填啥。如果 k > 后面的数字个数的阶乘。数一数，可以跳过几个阶乘数。

其实这个思路很像方法一的「剪枝」，只不过方法一就减法，方法二用除法。事实上，方法二要维护数组的有序性，所以时间复杂度不变。根据以上思路，设计算法流程如下：

算法流程设计：

  • 把候选数放在一个 有序列表 里，从左到右根据「剩下的数的阶乘数」确定每一位填谁，公式 k / (后面几位的阶乘数) 的值 恰好等于候选数组的下标；
  • 选出一个数以后，k 就需要减去相应跳过的阶乘数的倍数；
  • 已经填好的数需要从候选列表里删除，注意保持列表的有序性（因为排列的定义是按照字典序）；
  • 由于这里考虑的是下标，第 k 个数，下标为 k - 1，一开始的时候，k–。
    每次选出一个数，就将这个数从列表里面拿出。这个列表需要支持频繁的删除操作，因此使用双链表。在 Java 中 LinkedList 就是使用双链表实现的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.util.LinkedList;
import java.util.List;

public class Solution {

    public String getPermutation(int n, int k) {
        // 注意：相当于在 n 个数字的全排列中找到下标为 k - 1 的那个数，因此 k 先减 1
        k --;

        int[] factorial = new int[n];
        factorial[0] = 1;
        // 先算出所有的阶乘值
        for (int i = 1; i < n; i++) {
            factorial[i] = factorial[i - 1] * i;
        }

        // 这里使用数组或者链表都行
        List<Integer> nums = new LinkedList<>();
        for (int i = 1; i <= n; i++) {
            nums.add(i);
        }

        StringBuilder stringBuilder = new StringBuilder();

        // i 表示剩余的数字个数，初始化为 n - 1
        for (int i = n - 1; i >= 0; i--) {
            int index = k / factorial[i] ;
            stringBuilder.append(nums.remove(index));
            k -= index * factorial[i];
        }
        return stringBuilder.toString();
    }
}

题解出自@liweiwei1419

最后，不经历风雨,怎能在计算机的大山之顶看见彩虹呢！ 无论怎样，相信明天一定会更好！！！！！

-------------本文结束感谢您的阅读-------------
云澈 wechat
扫一扫，用手机访问哦
坚持原创技术分享，您的支持将鼓励我继续创作！
0%