二分查找_leetcode.410_分割数组的最大值

🌸题目

🍁给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。

注意:
数组长度 n 满足以下条件:

1 ≤ n ≤ 1000
1 ≤ m ≤ min(50, n)
示例:

输入:
nums = [7,2,5,10,8]
m = 2

输出:
18

解释:

1
2
3

一共有四种方法将nums分割为2个子数组。
其中最好的方式是将其分为[7,2,5] 和 [10,8]，
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

🌸分析思路

🍁这道题要找一个整数，这个整数有确定的范围，因此可以考虑使用二分查找，类似的典型问题有「力扣」第 69 题：平方根，「力扣」第 287 题：寻找重复数。

题目要求的变量（各自分组的和的最大值 M）与另一个变量（组数）有相关关系（负线性相关），而题目对组数有限制，根据这个相关关系去逼近 M 的最小值，这也是一类常见的使用「二分查找」的题型：「力扣」第 875 题：爱吃香蕉的珂珂。

重点理解：

大于的时候舍弃，小于等于的时候保留，这样左右向中间逼近能找到 M 的最小值，具体可以看题解中唯一的那张图；
理解贪心算法的应用，在从左向右划分组的时候，我们的方案是尽量让一个组有更多的元素，直至超过了设定的临界值

🌸方法：二分查找

🍁注意题目中给出的这 3 个条件：

数组中的元素均是「非负整数」；
子数组的特点是：「非空」且「连续」；
恰好分成 m 个非空「非空连续子数组」。

题目中还给出了一个概念：「连续子数组各自和的最大值」，我们用一个变量 maxIntervalSum 表示。不难知道：

每一个「非空连续子数组」如果包含的元素个数越多，那么 maxIntervalSum 就可能越大（非负整数保证）；
一个 maxIntervalSum的数值就唯一对应了一个分出的「非空连续子数组」的组数 M ，它们是函数关系（一一对应）， maxIntervalSum 是自变量，M 是因变量，可以写成：
M = function(maxIntervalSum)

如何找到一个 maxIntervalSum，使得它对应的 M 恰好等于题目给出的 m。但是我们容易分析出，这个函数是一个单调递减的函数：

如果 maxIntervalSum 越小，分出的「非空连续子数组」的组数 M 就越大；
如果 maxIntervalSum 越大，分出的「非空连续子数组」的组数 M 就越小。

因此这个函数是单调不增的函数。

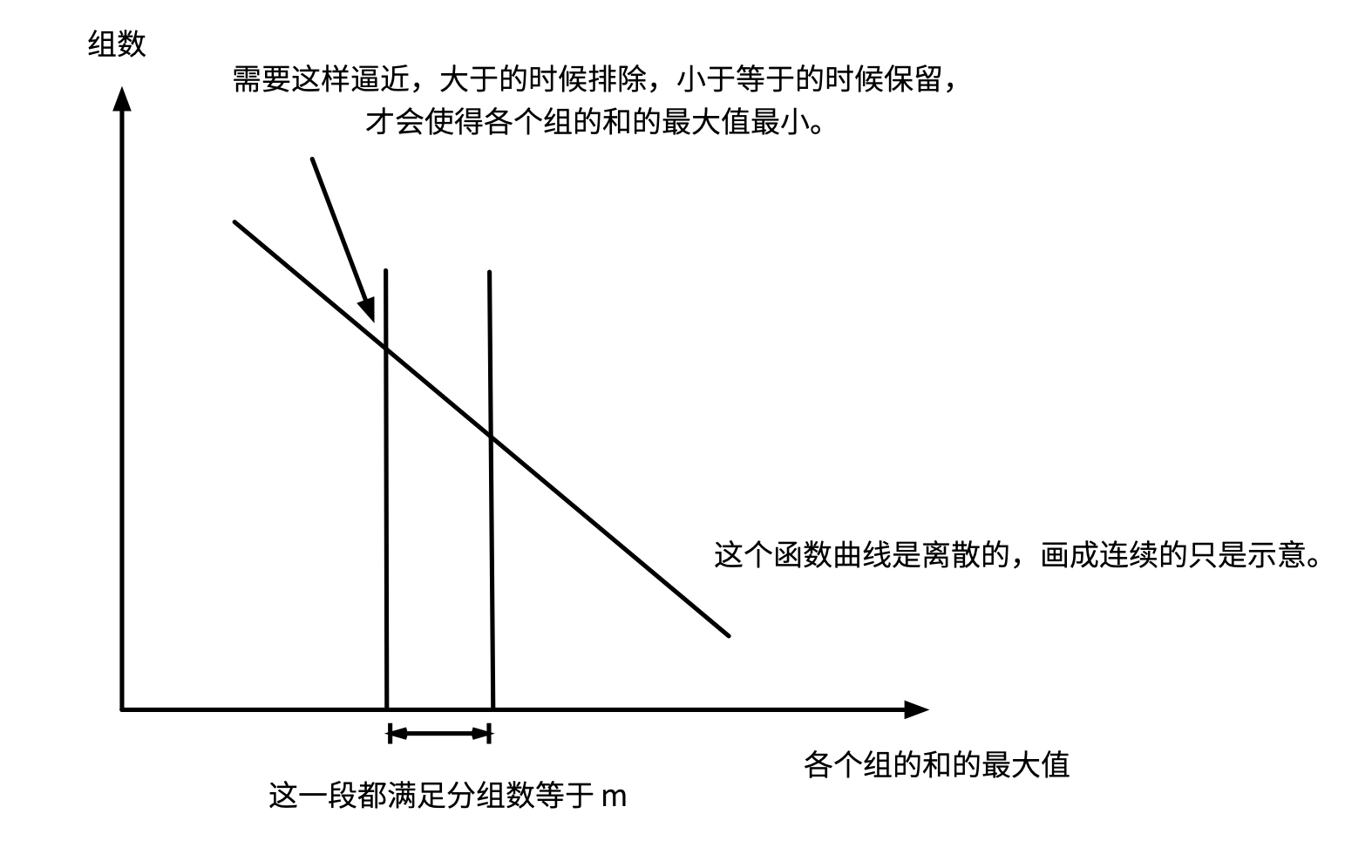
原因就在于上面强调的题目中给出的 2 个条件：非负整数和非空连续子数组，由于这种单调性，可以使用二分查找，找到与 m 对应的 maxIntervalSum 。

参考代码：

下面是一些细节：

只要连续加起来的数值超过了 maxIntervalSum，就新产生一个新的连续子数组；
maxIntervalSum 的最小值是这个数组中的最大值，这是因为 max(nums) 一定会被分到其中一组；
maxIntervalSum 的最大值是这个数组中所有元素的和，极端情况就是题

目中给出 m = 1 的时候。

public int splitArray(int[] nums, int m) {
	int max = 0;
	int sum = 0;
	
	// 计算「子数组各自的和的最大值」的上下界
	for(int num : nums) {
		max = Math.max(max, num);
		sum += num;
	}
	
       // 使用「二分查找」确定一个恰当的「子数组各自的和的最大值」，
       // 使得它对应的「子数组的分割数」恰好等于 m
	int left = max;
	int right = sum;
	while(left < right) {
		int mid = left + (right - left) / 2;
		
		int splits = split(nums, mid);
		if(splits > m) {
               // 如果分割数太多，说明「子数组各自的和的最大值」太小，此时需要将「子数组各自的和的最大值」调大
               // 下一轮搜索的区间是 [mid + 1, right]处。
			left = mid + 1;
		}else {
			 // 下一轮搜索的区间是上一轮的反面区间 [left, mid]
			right = mid;
		}
	}
	return left;
}
   /***
   *
   * @param nums 原始数组
   * @param maxIntervalSum 子数组各自的和的最大值
   * @return 满足不超过「子数组各自的和的最大值」的分割数
   */
private int split(int[] nums, int maxIntervalSum) {
	// TODO Auto-generated method stub
	//至少一个分割数
	int splits = 1;
	//当前区间的和
	int curIntervalSum = 0;
	for(int num : nums) {
		if(curIntervalSum + num > maxIntervalSum) {
			curIntervalSum = 0;
			splits++;
		}
		curIntervalSum += num;
	}
	return splits;
}

python

class Solution:
    def splitArray(self, nums: list[int], m: int) -> int:
        def split(nums: list[int], maxIntervalSum: int) -> int:
            splits = 1
            curIntervalSum = 0
            for num in nums:
                if curIntervalSum + num > maxIntervalSum:
                    curIntervalSum = 0
                    splits += 1
                curIntervalSum += num
            return splits
        
        
        #   计算「子数组各自的和的最大值」的上下界
        _max = max(nums)
        _sum = sum(nums)
        #  使用「二分查找」确定一个恰当的「子数组各自的和的最大值」，
        # 使得它对应的「子数组的分割数」恰好等于 m
        left, right = _max, _sum
        while(left < right):
            mid = left + (right - left) / 2
            
            splits = split(nums, mid)
            if splits > m:
                left = mid + 1
            else:
                right = mid
        return left

🌸总结

🍁理解单调性

一个重要的性质：分割数越大，「子数组各自的和的最大值」就越小（非递增，满足单调性），因此可以使用二分查找，定位分割数；
一种「分割方案（分成几个子数组）」对应了一个「子数组各自的和的最大值」；
反过来，一个「子数组各自的和的最大值」对应了一种「分割方案（分成几个子数组）」；
它们是一一对应的关系（关键）。

🍁思路整理（绕了个弯子去逼近）

先找「子数组各自的和的最大值」的中间数（尝试得到的一个值），看看它对应的「分割方案（分成几个子数组）」是多少；
如果「分割方案（分成几个子数组）」比题目要求的 m 还多，说明「子数组各自的和的最大值」还太小，所以下一次搜索应该至少是中位数 + 1（left = mid + 1），它的反面即至多是中位数（right = mid）。